The domain of a function is the
complete set of possible values of the independent variable in the
function. The domain of a function is the set of all possible x
values which will make the function "work" and will output real
y-values.
The function
y = √(x
+ 4) has the following graph.
The
Graph of a Function
The graph of
a function is the set of all points whose co-ordinates (x, y)
satisfy the function y = f(x). This means that for each x-value
there is a corresponding y-value which is obtained when we substitute
into the expression for f(x).
Since there
is no limit to the possible number of points for the graph of the function, we
will follow this procedure at first:
- Select a few values of x
(at least 5)
- Obtain the corresponding values
of the function and enter them into a table
- Plot these points by joining
them with a smooth curve
Example : Graph the function y = x −x2
(a)
Determine the y-values for a typical set of x-values and write
them in a table.
|
|
-2
|
-1
|
0
|
1
|
2
|
3
|
|
|
-6
|
-2
|
0
|
0
|
-2
|
-6
|
Range
The range
of a function is the complete set of all possible resulting values
of the dependent variable of a function, after we have substituted the
values in the domain. The range of a function is the possible y
values of a function that result when we substitute. all the possible x-values
into the function.
|
When
finding the range, remember:
- Substitute different x-values
into the expression for y to see what is happening
- Make sure you look for minimum
and maximum values of y
- Draw a sketch! In math,
it's very true that a picture is worth a thousand words.
|
Example : Find
the domain and range for the function defined as
f(x) = x2 + 4 for x
> 2
The function
f(x) has a domain of "all real numbers, x >
2" as defined in the question.To find the range:
- When x = 2, f(2)
= 8
- When x increases from 2,
f(x) becomes larger than 8
Hence, the range
is "all real numbers, f(x) > 8"
Here is the
graph of the function, with an open circle at (2, 8) indicating that the
domain does not include x = 2 and the range does not include f(2)
= 8.
2.2 Special Function
Constant
Function
- Constant Function is a linear
function of the form y = b, where b is a constant.
- It is also written as f(x)
= b.
-
A Function of the form h (x) = c, where c is a
constant, is a called Constant
Function
|
The
graph of a Constant Function is a horizontal line.
Polynominal Functions
f(x) = 5x2 - 2
f(x+h) = 5(x+h)2 - 2 = 5( x2
+ 2xh + h2 ) - 2 = 5x2 + 10xh + 5h2 - 2
f(x+h) - f(x) = 5( x2
+ 2xh + h2 ) - 2 = 5x2 + 10xh + 5h2 - 2 -
( 5x2 - 2 )
f(x+h) - f(x) = 5x2
+ 10xh + 5h2 - 2 - 5x2 + 2 = 10xh + 5h2
f(x+h) - f(x) = h ( 10x
+ 5h)
a.
3 _ 6
2 + 7 is a polynomial (function) of a
degree with leading coefficient1
|
A Function that is
polynomial functions is called a Rational Function
f(x)
= 3 / x
f(x+h)
= 3 / (x+h)
f(x+h) - f(x) = 3 / (x+h) - 3 / x
f(x+h) - f(x) = 3 x / [ x(x+h)] - 3(x+h) / [x(x+h)]
f(x+h) - f(x) = ( 3x - 3x - 3h ) / [ x(x+h) ]
f(x+h) - f(x) = -3h / [x(x+h)]
[f(x+h)
- f(x)] / h = -3h / [x(x+h)] / h = -3 / [ x(x+h) ]
In mathematics a rational function is any function which can be
written as the ratio of two polynomial functions . Neither the coefficient of
the polynomials nor the values taken by the function are necessarily rational.
Case-Define Function
In mathematics,
a function associates one quantity, the argument of the function, also known as the input, with
another quantity, the value of the function, also known as the output. A
function assigns exactly one output to each input. f(x) is said, "F of
X." The argument and the value may be real numbers,
but they can also be elements from any given set. An example of a function is f(x) = 2x,
a function which associates with every number the number twice as large. Thus,
with the argument 5 the value 10 is associated, and this is written f(5)
= 10
Factorials
In mathematics,
the factorial of a non-negative
integer n, denoted by n!,
is the product of all positive integers less than or equal to n.
|
Example
- 4! =
4 × 3 × 2 × 1 = 24
- 7! =
7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
- 1! =
1
2.3 Combinations of Functions
|
The sum,
difference, product, or quotient of functions can be found easily.
Sum
(f + g)(x) = f(x) + g(x)
Difference
(f - g)(x) = f(x) - g(x)
Product
(f · g)(x) = f(x) · g(x)
Quotient
(f / g)(x) = f(x) / g(x), as
long as g(x) isn't zero.
The domain of each of these combinations is the intersection of the domain
of f and the domain of g. In other words, both functions must be defined at a
point for the combination to be defined. One additional requirement for the
division of functions is that the denominator can't be zero, but we knew that
because it's part of the implied domain.
Basically what the above says is that to evaluate a combination of
functions, you may combine the functions and then evaluate or you may evaluate
each function and then combine.
Example :
n the following examples, let f(x) = 5x+2 and g(x) = x2-1.
We will then evaluate each combination at the point x=4. f(4)=5(4)+2=22 and
g(4)=42-1=15
|
Expression
|
Combine, then evaluate
|
Evaluate, then combine
|
|
(f+g)(x)
|
(5x+2) + (x2-1)
=x2+5x+1
|
(f+g)(4)
|
42+5(4)+1
=16+20+1
=37
|
f(4)+g(4)
|
22+15
=37
|
|
(f-g)(x)
|
(5x+2) - (x2-1)
=-x2+5x+3
|
(f-g)(4)
|
-42+5(4)+3
=-16+20+3
=7
|
f(4)-g(4)
|
22-15
=7
|
|
(f·g)(x)
|
(5x+2)*(x2-1)
=5x3+2x2-5x-2
|
(f·g)(4)
|
5(43)+2(42)-5(4)-2
=5(64)+2(16)-20-2
=330
|
f(4)·g(4)
|
22(15)
=330
|
|
(f/g)(4)
|
(5x+2)/(x2-1)
|
(f/g)(4)
|
[5(4)+2]/[42-1]
=22/15
|
f(4)/g(4)
|
22/15
|
Composition
of Functions
While
the arithmetic combinations of functions are straightforward and fairly
easy, there is another type of combination called a composition.
A
composition of functions is the applying of one function to another
function. The symbol of composition of functions is a small circle between
the function names. I can't do that symbol in text mode on the web, so I'll
use a lower case oh "o" to represent composition of functions.
- (fog)(x) = f [ g(x) ]
- These are read "f composed
with g of x" and "g composed with f of x" respectively
(gof)(x) = g [ f(x)
The function
on the outside is always written first with the functions that follow being on
the inside. The order is important. Composition of functions is not
commutative.
Examples
of Composition of Functions
That doesn't
sound that bad. Let's look at a few examples.
f(x)=5x+2
and g(x)=x2-1
- (fog)(x) = f [ g(x) ] = f [ x2-1
] = 5( x2-1 ) + 2 = 5x2- 5 + 2 = 5x2-3
- (gof)(x) = g [ f(x) ] = g [
5x+2 ] = ( 5x+2 )2 - 1 = 25x2 + 20x + 4 - 1 = 25x2
+ 20x + 3
f(x) =
sqrt(x) and g(x) = 4x2
- (fog)(x) = f [ g(x) ] = f [ 4x2
] = sqrt( 4x2 ) = 2 | x |
- (gof)(x) = g [ f(x) ] = g [
sqrt(x) ] = 4 ( sqrt(x) )2 = 4x, x ≥ 0
f(x) =
sqrt(x-4) and g(x) = 1 - x2
- (fog)(x) = f [ g(x) ] = f [ 1-x2
] = sqrt ( [1-x2] - 4 ) = sqrt ( -x2 - 3 ) = ø
- (gof)(x) = g [ f(x) ] = g [
sqrt(x-4) ] = 1 - [ sqrt(x-4) ]2 = 1 - ( x-4 ) = 5 - x, x ≥ 4
If the last
example needed some explanation, then this one definitely needs some, too.
Let's take the easier one (gof)(x) first. There was an implied domain of x ≥ 4
because of the square root, but after squaring it, it was no longer implied, so
it needed to be stated explicitly.
Okay, now
for the harder one (fog)(x). I'll give the simple explanation here and the more
complete one later. After simplifying, you got the square root of (-x2
- 3). -x2-3 is always negative, no matter what real number x is, and
you can't take the square root of a negative number, so it is always undefined
(for the set of reals)
Finding Domains on Composition of Functions
When you
find a composition of a functions, it is no longer x that is being plugged into
the outer function, it is the inner function evaluated at x. So there are two
domains that we have to be concerned about. If we consider (fog)(x), we see
that g is evaluated at x, so x has to be in the domain of g. We also see that f
is evaluated at g(x), so g(x) has to be in the domain of f.
- For (fog)(x), x is a value that
can be plugged into g and gives you a value g(x) that can be plugged into
f to get f(g(x))
- For (gof)(x), x is a value that
can be plugged into f and gives you a value f(x) that can be plugged into
g to get g(f(x)).
But, it's
not as bad as it looks, either. Let's consider that last example again.
|
Function
|
Domain
|
Range
|
|
f(x) = sqrt(x-4)
|
x ≥ 4
|
y ≥ 0
|
|
g(x) = 1-x2
|
All reals
|
y ≤ 1
|
When you
find (fog)(x), there are two things that must be satisfied:
- x must be in the domain of g,
which means x is a real number (pretty easy to do)
- g(x) must be in the domain of
f, which means that 1-x2^2 ≥ 4 (when you try to solve this, you
get the empty set)
|
|
2.4 Inverse Functions
Before defining the inverse of a function we need to have the right mental
image of function.
Consider the function f(x) = 2x + 1. We know how to
evaluate f at 3, f(3) = 2*3 + 1 = 7. In this section it helps to think of f as
transforming a 3 into a 7, and f transforms a 5 into an 11
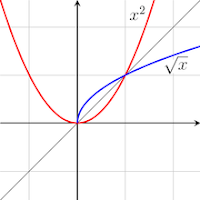
Let g(x) = (x - 1)/2. Then g(7) = 3, g(-3) = -2, and g(11) = 5, so g seems
to be undoing what f did, at least for these three values. To prove that g is
the inverse of f we must show that this is true for any value of x in the
domain of f. In other words, g must take f(x) back to x for all values of x in
the domain of f. So, g(f(x)) = x must hold for all x in the domain of f. The
way to check this condition is to see that the formula for g(f(x)) simplifies
to x.
g(f(x)) = g(2x + 1) = (2x + 1 -1)/2 = 2x/2 = x.
This simplification shows that if we choose any number and let f act it,
then applying g to the result recovers our original number. We also need to see
that this process works in reverse, or that f also undoes what g does.
f(g(x)) = f((x - 1)/2) = 2(x - 1)/2 + 1 = x - 1 + 1 = x.
Letting f-1 denote the inverse of f, we have just shown that g =
f-1.
Definition:
Let f and g be two functions. If
f(g(x)) = x and g(f(x)) = x,
then g is the inverse of f and f is the inverse of g.
Exercise 1:
(a) Open the
Java Calculator and enter the formulas for f and g. Note that
you take a cube root by raising to the (1/3), and you do need to enter the
exponent as (1/3), and not a decimal approximation. So the text for the g box
will be
(x
- 2)^(1/3)
Use the calculator to evaluate f(g(4)) and g(f(-3)). g is the
inverse of f, but due to round off error, the calculator may not return the
exact value that you start with. Try f(g(-2)). The answers will vary for
different computers. However, on our test machine f(g(4)) returned 4; g(f(-3)) returned
3; but, f(g(-2)) returned -1.9999999999999991, which is pretty close to -2.
The calculator can give us a good indication that g is the inverse of f, but
we cannot check all possible values of x.
Graphs of Inverse Functions
|
|
We have seen examples of reflections in
the plane. The reflection of a point (a,b) about the x-axis is (a,-b), and
the reflection of (a,b) about the y-axis is (-a,b). Now we want to reflect
about the line y = x
|
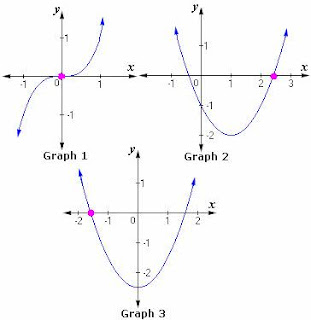
Existence of an Inverse
|
|
Some functions do not have inverse
functions. For example, consider f(x) = x2. There are two
numbers that f takes to 4, f(2) = 4 and f(-2) = 4. If f had an inverse,
then the fact that f(2) = 4 would imply that the inverse of f takes 4 back
to 2. On the other hand, since f(-2) = 4, the inverse of f would have to
take 4 to -2. Therefore, there is no function that is the inverse of f.
2.5 Graph in
Rectangular Coordinates
An x-intercept of the graph of an equation in x and y is
a point where the graph intersects the x-axis. A y-intercepts is a point
where the graph intersects the y-axis
|
rectangular coordinate system, ordered pairs and solutions to equations
in two variables. For example, you may have a cost function that is
dependent on the quantity of items made. If you needed to show your boss
visually the correlation of the quantity with the cost, you could do that on a
two-dimensional graph.
Intercepts
and Graph
The x-intercept of a line is the point
at which the line
crosses the x axis. ( i.e. where the y value equals 0 )
x-intercept = ( x, 0 )
The y-intercept of a line is the point
at which the line
crosses the y axis. ( i.e. where the x value equals 0 )

2.6
Symmetry
Symmetry
is when one shape becomes exactly like another if you flip, slide or turn
it.
The simplest type of Symmetry is "Reflection" (or
"Mirror") Symmetry, as shown in this picture of my dog Flame.
and in a graph
2.7 Translaction and Reflection
The word transform means "to change." In
geometry, a transformation changes the position of a shape on a coordinate
plane. What that really means is that a shape is moving from one place to
another. There are three basic transformations:
- Flip (Reflection) -A
FLIP takes place when a shape is flipped across a line and faces the
opposite direction. Because the shape ends up facing the opposite
direction, it appears to be reflected, as in a mirror. Hence the name
REFLECTION.
- Slide (Translation)
-
Moving a shape, without rotating or flipping
it. "Sliding".the shape till looks exactly the same, just in a different place
Turn
(Rotation)
A
circular movement.
There is a central point that stays fixed and everything else moves around that
point in a circle
|
|
|







